Mathematica works in the interactive mode by taking input at the In[number]:= statement and then performing the requested operation and giving the result in an Out[number] statement. In Mathematica the percent sign (%) refers to the output of the previous command and Out[ number ] or % number can be used in any subsequent command as input for another command. For example, the command In[1]:= 6 results in Out[1]=6. You could then use the command In[2]:=Out[1]+5 or In[2]:=%1+5 that would result in Out[2]=11. The colon and equal sign (:= ) allow you to define variables. For example In[3]:=x:=5 would assign the value 5 to the variable x. The current value of any variable can be retrieved by typing its name at an In line. In Mathematica, functions act on arguments that are inside square brackets [] , lists are contained in curly brackets {} , and parentheses are used for grouping.
Computations and Functions
Mathematica can perform simple computations such as addition (+ ), subtraction (- ), multiplication (* or , In[1]:=6 7 results in 42), division (/ ), and exponents (^ ) along with numerous built-in functions. Mathematica can perform these operations on both numerical and symbolic representations. The following examples demonstrate several of Mathematica’s useful algebra and calculus functions:
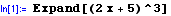
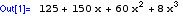
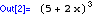
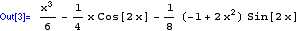
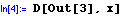
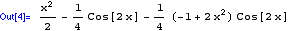
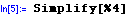


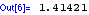
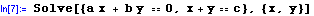
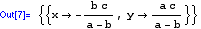
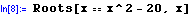
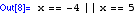
Expand
expands all multiplication and power terms in an algebraic expression.
Factor
factors a polynomial over the integers. Note the use of the % sign denoting the output from the previous command.
Integrate
returns the indefinite integral with respect to the selected variable(s). The integrate command can also be used to determine a definite integral using
Integrate[expr, {x, xmin, xmax}]
D
differentiates an expression with respect to the selected variable(s).
Simplify
performs algebraic manipulations to return the simplest form it can find.
N
returns approximate results using a specific number of significant digits.
Solve
solves an equation or system of equations for selected variables. Use the double equal sign (==) to define an equation.
Roots
finds the roots of the equation with respect to the selected variable.
Plotting in Mathematica
Mathematica supports numerous plot types and formatting options. To create simple x-y plots you can use the Plot command, for example:
Plot[ Sin[Exp[x]], {x, 0, Pi}] would plot the function y=sin(exp(x)) from 0 to pi.
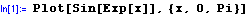
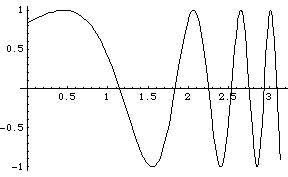
The command Show allows you to modify the display in a graphics window. For example, the commandShow[ %, Frame -> True, FrameLabel -> {"Time", "Signal"}] would add a frame and labels to the previous plot (note the % ).
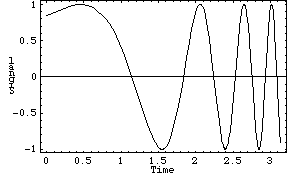
These items are referred to as plot options. Plot options can also be added in the Plot command, Plot[x^2, {x,0,10}, Frame -> True]. More than one graph can be plotted on a single axis using the Plot command with a list of functions, Plot[{f1, f2, ...}, {x,xmin,xmax}]. The following commands can also be used in place of Plot for appropriate plot types: LogPlot, LogLogPlot, PolarPlot, Plot3D, ContourPlot. To determine the syntax and default options for any of the plot commands you can type ?? commandname, for example ??LogPlot.
Using Mathematica in Text Mode on Unix
Mathematica can also be run in text mode in Unix or Xwin environment. The commands demonstrated above are also valid in text mode.
Sourcing the setup files
At USC we have developed short setup files that set an appropriate path for the software you are using. You need to source these setup files in order for the software to work properly.
You can source the setup files at a UNIX prompt or add a few lines to your .login file that will source the setup files at login. To source the setup files at a UNIX prompt use the command.
source /usr/usc/math/default/setup.csh
To source the setup files at login you need to add the appropriate lines to your .login file. These lines can be found in the file /usr/usc/math/default/README.USC